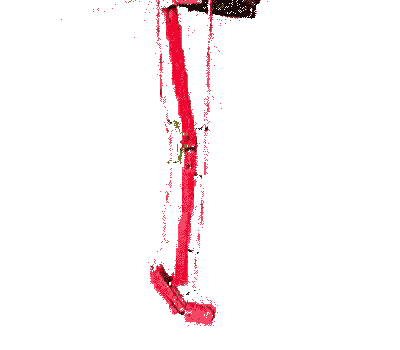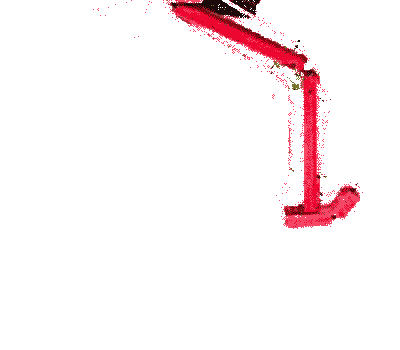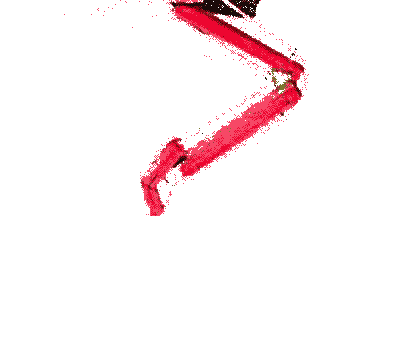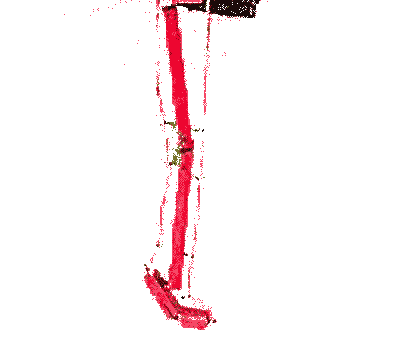|
|
| (Der Versionsvergleich bezieht 8 dazwischenliegende Versionen mit ein.) |
| Zeile 28: |
Zeile 28: |
| | | | |
| | | | |
| - | =Strandbeester=
| |
| | | | |
| - | Der Künstler [[Jansen Theo|Theo Jansen]] hat für seine Strandbeester eine besondere Kinematik entwickelt, die einfach modifiziert werden kann. Die Funktionsweise lässt sich mit der JavaScript Bibliothek JSXGraph visualisieren:
| |
| - |
| |
| - | <jsxgraph box="Diagramm_in_the_box" width="600" height="600">
| |
| - | var brd = JXG.JSXGraph.initBoard('Diagramm_in_the_box',{boundingbox:[-120,50,50,-50], axis:false, grid:false, showCopyright:false, showNavigation:false, keepaspectratio: true });
| |
| - | var p0 = brd.create('point', [0,0], {withLabel:false, fixed:true, size:3, strokeColor:"black", fillColor:"#58FA58"});
| |
| - | var p1 = brd.create('point', [-38,-7.8], {withLabel:false, fixed:true, size:3, strokeColor:"black", fillColor:"#58FA58"});
| |
| - | var pc1 = brd.create('point', [0,-7.8], {withLabel:false, fixed:true, size:1, strokeColor:"white", fillColor:"#BDBDBD"});
| |
| - | var d1 = brd.create('segment', [p1, pc1], {withLabel:true, name:'a', strokeColor:"#BDBDBD"});
| |
| - | var d2 = brd.create('segment', [p0, pc1], {withLabel:true, name:'l', strokeColor:"#BDBDBD"});
| |
| - | var c1 = brd.create('circle',[p1,41.5],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"});
| |
| - | var ca = brd.create('circle',[p0,15],{strokeColor:'#D8D8D8', strokeOpacity:1, fillColor:'#E6E6E6', highlightFillColor:"#E6E6E6"});
| |
| - | p2 = brd.create('glider',[0,15,ca], {name:'Diesen Punkt ziehen', size:4, strokeColor:"red", fillColor:"red"}),
| |
| - | d3 = brd.create('segment', [p0, p2], {withLabel:true, name:'m', strokeColor:"#BDBDBD"}),
| |
| - | c2 = brd.create('circle',[p2,50],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"black", highlightStrokeOpacity:"100"}),
| |
| - | p3 = brd.create('intersection', [c1, c2, 1], {withLabel:false, size:1, strokeColor:"#A4A4A4", fillColor:"#A4A4A4"}),
| |
| - | b1 = brd.create('segment', [p1, p3], {withLabel:true, name:'b'}),
| |
| - | b2 = brd.create('segment', [p2, p3], {withLabel:true, name:'j'}),
| |
| - | c3 = brd.create('circle',[p3,55.8],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | c4 = brd.create('circle',[p1,40.1],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | p4 = brd.create('intersection', [c3, c4, 0], {withLabel:false, size:1, strokeColor:"#A4A4A4", fillColor:"#A4A4A4"}),
| |
| - | b3 = brd.create('segment', [p3, p4], {withLabel:true, name:'e'}),
| |
| - | b4 = brd.create('segment', [p1, p4], {withLabel:true, name:'d'}),
| |
| - | c5 = brd.create('circle',[p1,39.3],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | c6 = brd.create('circle',[p2,61.9],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | p5 = brd.create('intersection', [c5, c6, 0], {withLabel:false, size:1, strokeColor:"#A4A4A4", fillColor:"#A4A4A4"}),
| |
| - | b5 = brd.create('segment', [p1, p5], {withLabel:true, name:'c'}),
| |
| - | b6 = brd.create('segment', [p2, p5], {withLabel:true, name:'k'}),
| |
| - | c7 = brd.create('circle',[p5,36.7],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | c8 = brd.create('circle',[p4,39.4],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | p6 = brd.create('intersection', [c7, c8, 1], {withLabel:false, size:1, strokeColor:"#A4A4A4", fillColor:"#A4A4A4"}),
| |
| - | b7 = brd.create('segment', [p4, p6], {withLabel:true, name:'f'}),
| |
| - | b8 = brd.create('segment', [p5, p6], {withLabel:true, name:'g'}),
| |
| - | c9 = brd.create('circle',[p5,49],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | c10= brd.create('circle',[p6,65.7],{strokeColor:'#D8D8D8', strokeOpacity:0, highlightStrokeColor:"white", highlightStrokeOpacity:"0"}),
| |
| - | p7 = brd.create('intersection', [c9, c10, 1], {withLabel:false, size:1, strokeColor:"red", fillColor:"white", trace:true}),
| |
| - | b9 = brd.create('segment', [p5, p7], {withLabel:true, name:'i'}),
| |
| - | b10= brd.create('segment', [p6, p7], {withLabel:true, name:'h'}),
| |
| - | p8 = brd.create('point', [-180,-93], {withLabel:false, fixed:true, size:3, strokeColor:"white", fillColor:"white"}),
| |
| - | p9 = brd.create('point', [180,-93], {withLabel:false, fixed:true, size:3, strokeColor:"white", fillColor:"white"}),
| |
| - | li = brd.create('line',[p8,p9], {strokeColor:'#D8D8D8',strokeWidth:2});
| |
| - |
| |
| - | </jsxgraph>
| |
| - |
| |
| - |
| |
| - |
| |
| - | Quelle: http://library.fridoverweij.com/graph/strandbeest/strandbeest.html
| |
| - |
| |
| - | Video mit Varianten der Strandbiester:
| |
| - |
| |
| - | https://m.youtube.com/watch?v=kKSDgIhc8GI Gleiches Prinzip - unterschiedliche Geometrie : Vielfalt der Bewegung [[Jansen Theo]]
| |
| - |
| |
| - | siehe auch [[Bionik]]
| |
| | | | |
| | [[Kategorie:Technik]] | | [[Kategorie:Technik]] |
In der Robotertechnik ist die Bewegung von Manipulatoren eine der wesentlichen Aufgabenstellungen. Ein Werkzeug muss sicher im Raum bewegt werden. Dies geschieht üblicherweise durch Motore, die komplexe Gelenksysteme bewegen. Dabei werden die Bewegungsabläufe häufig in Einzelbewegungen zerlegt, wodurch eine unnatürlich abgehackte Bewegung entsteht. Anhand von komplexen Koordinatenberechnungen, werden die Motoren angesteuert. In natürlichen Systemen von Lebewesen erfolgt in der Regel keine Zerlegung der Bewegung. Der Bewegungsaparat bildet ein komplexes System aus Gelenken, festen Stützen (Skelett) und Zugelementen (Muskeln). Durch die mechanische Kopplung ergibt sich der Bewegungsablauf durch das System selbst, wobei die Zugelemente die erforderlichen Kräfte und Verschiebungen in das System einbringen.
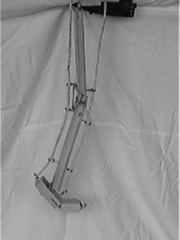
habe ich das Modell eines menschlichen Beines aus Holzstäben, Scharnieren und Seilen nachgebildet
. Bereits bei diesem einfachen Modell lassen sich nur durch 2 lineare Zugbewegungen an den Seilenden komplexe Bewegungsabläufe erzeugen. Dabei sind für den Bewegungsablauf folgende Parameter wichtig:
In einem natürlichen System würden Gelenkstellung und die Position der Zugelemente über neuronale Strukturen verarbeitet und zur Ansteuerung der Zugelemente zurück geführt.
Technisch interessant ist bei dem "natürlichen" Konzept die saubere Trennung zwischen Zug- und Druckkräften. Der "Antrieb" erfolgt ausschließlich durch Variation der Zugkräfte. Das System selbst kann durch Auswahl der Werkstoffe und Dimensionierung der verschiedenen Elemente sehr genau an die auftretenden Belastungen angepasst werden.